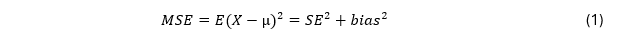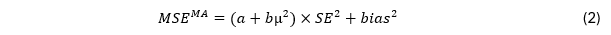Low(er) precision of estimators of selection models: intuition and a preliminary analysis
This blogpost has been written by Marcel van Assen. Marcel is a professor of our research group that focuses his research on statistical methods to combine studies, publication bias, questionable research practices, fraud, reproducibility, improving pre-registration & registered reports.
Estimates of random-effects meta-analysis are negatively affected by publication bias, generally leading to overestimation of effect size. Selection models address publication bias and can yield unbiased estimates of effects, but the precision of their estimates is lower than of random-effects meta-analysis. Why and how much precision is lowered has been unclear, and I here provide an intuition and analysis to preliminarily answer these questions. If you are not interested in the details of the analysis, please go directly to the conclusions below.
1. Accurately estimating effect size with selection models in the context of publication bias
Meta-analysis is used to statistically synthesize information of different studies on the same effect. Each of these studies yields one or more effect sizes, and random-effects meta-analysis combines these effect sizes into one estimate of the average true effect size and an estimate of the variance or heterogeneity of the effect size.
A well-known and serious problem of both the scientific literature and meta-analyses is publication bias. Typically, publication bias amounts to the overrepresentation of statistically significant findings in the literature, or alternatively, the underrepresentation of nonsignificant findings. Because of publication bias meta-analyses generally overestimate the true effect size, and in case of a true zero effect size publication bias likely results in a false positive. Both these consequences are undesirable; we need an accurate estimate of the effectives of an intervention for adequate cost-benefit analyses, and implementing interventions that do not work is very harmful.
One solution of the problem is applying meta-analysis using models that account for the possible effects of publication bias. For example, selection models (e.g., Hedges and Vevea, 2005), including p-uniform* (van Aert & van Assen, 2025). Characteristic of these models is that they categorize effect sizes into at least two different intervals, and that estimation occurs by treating both intervals independently. In the most parsimonious variant of these models, two intervals of effect sizes are distinguished, for instance “effect sizes statistically significant at p < .025, right-tailed” and “other effect sizes”. The critical assumption in all these models is then that the probability of publication of effect sizes within one interval is constant but may differ across different intervals. Indeed, if this assumption holds, and all intervals contain at least some effect sizes, and there is publication bias, selection models and p-uniform* accurately estimate average effect size as well as heterogeneity of effect size (e.g., Hedges & Vevea, 2005; van Aert & van Assen, 2025). Problem solved?
2. Accurate estimation with selection models comes at a prize: less precision
The price that we pay for accurate estimation with selection models is lower precision of the estimates. Consider the following two examples to consider if we are willing to pay this price. The field of both examples is plagued with publication bias. Hence it can be expected that random-effects meta-analysis overestimates effect size,
In example A the random effects meta-analysis yields an estimated Hedges’ g = 0.7 with SE = 0.1, whereas a selection model yields an estimate equal to 0.6 with SE = 0.2. Both models strongly suggest that the true effect is positive, although the selection model’s estimate is somewhat lower and considerably less precise.
In example B we obtain Hedges’ g = 0.25 with SE = 0.1 using random-effects meta-analysis and with a selection model we obtain estimate -0.12 with SE = 0.3. Here, random-effect meta-analysis suggests a small and positive true non-zero effect size (z = 2.5, p = .012), whereas the selection model doesn’t lead to a rejection of the null-hypothesis.
The performance of estimators is evaluated using different criteria. One criterion is bias. Concerning bias, selection models outperform random-effects meta-analysis. But as we also prefer precision, we may also use another criterion that combines bias and precision. A criterion that does that is the mean squared error (MSE)
with X being the estimator of parameter µ, and bias equal to (E(X) - µ)^2) .
Let’s apply the MSE to both our examples. For example A, assume that = .6 and that random-effects meta-analysis overestimates with 0.1 because of publication bias. Then, MSE of random-effects meta-analysis equals .1 2 + .1 2 = .02, and MSE of the unbiased selection model equals .2 2 + 0 2 = .04, with random-effects meta-analysis being the “winner” with the lowest value of MSE. Concerning example B, assume that = .2 and the bias equals .2. Then, MSE = .1 2 + .2 2 = .05 for the regular meta-analysis, whereas it equals .3 2 + 0 2 = .09 for the selection model, with again random-effects meta-analysis being the “winner”.
I, however, want to argue that the MSE is not a good criterion to evaluate the performance of estimators of meta-analytic effect size in the context of publication bias. Where it is relatively inconsequential to pick one estimator over the other in example A as both point at a positive effect of considerable size, it is surely consequential in cases like situation B. If = 0, random-effects meta-analysis overestimates effect size with type I error rates (another relevant performance criterion) close to 1, rather than α, in case of publication bias (e.g., Carter et al., 2019); it provides a precise but very wrong estimate, leading to harmful conclusions about the effectiveness of interventions. Thus, the precision of estimators is important, but its accuracy is sometimes (much) more important. Perhaps we should use another performance criterion MSEMA for effect size estimators in meta-analysis, such as
with a and b being positive constants. Parameter a signifies the extent to which precision is taken into account in the calculation of MSE anyway, whereas b signifies how much of precision is taken into account depending on true effect size. For a = 1 and b = 0, MSE = MSEMA. Consider MSEMA with a = 0 and b = 4. Then, for = .5 it holds that MSEMA = MSE, but precision gets less emphasis relative to accuracy for < .5, with only accuracy being relevant for = 0. For the latter MSEMA, the random-effects estimator is preferred in Example 1 (1.44 × 0.12 + 0.12 = 0.0244 versus 1.44 × 0.22 = 0.0576), but the selection model estimator is preferred in Example 2 (0 × 0.22 + 0.22 = 0.04 versus 0 × 0.32 + 02 = 0). I argue that more research is needed in developing sensible alternatives to MSE in the context of meta-analysis with publication bias. Estimators belonging to class MSEMA may be a start in that direction.
3. Why the selection model’s effect size estimate is less precise: an intuitive explanation
To my knowledge, neither an intuition has been provided nor an examination has been conducted on the reasons for the lower precision of the selection model’s estimate. In this section I hope to provide some intuition, in the next section the results of a preliminary analysis.
Consider a random draw of four observations from a normal distribution with mean 0 and standard deviation 1:
set.seed help <- rnorm(4) x <- sort(help)
I initially selected seed 37, but with that seed I did not end up with two positive and two negative observations. Hence, I increased the seed by one, to obtain the following values of x:
-1.0556027 -0.2535911 0.0251569 0.6864966
Now, let us think about estimating µ, assuming a normal distribution with a variance equal to 1, or N(0,1). We can estimate µ using regular maximum likelihood estimation or using the approach of a selection model with two intervals, say one below and one above x = 0. For illustrative purposes, rather than estimating µ, we compare the fit or likelihood of the data for three values of µ (-1, 0, 1) for both approaches (regular, selection model). The selection model is based on two intervals, one for negative and one for positive values of x.
Figure 1 shows the four x-values and their likelihoods for the three values of µ for the regular approach, which are also presented in the following table:
| x | f(mu = 0) | f(mu = 1) | f(mu = 1) |
|---|---|---|---|
| -1.0556027 | 0.2285302 | 0.39832606 | 0.04823407 |
| -0.2535911 | 0.3863186 | 0.30194764 | 0.18182986 |
| 0.0251569 | 0.3988161 | 0.23588477 | 0.24805667 |
| 0.6864966 | 0.3151907 | 0.09622425 | 0.37981130 |
Figure 1: Likelihoods of four x-values (vertical lines) for models N(-1,1) in red, N(0,1) in green, N(1,1) in blue.
Note that particularly x = .686 is unlikely under µ = -1 (the red curve), and x = -1.056 is unlikely under µ = 1 (the blue curve). Because of this, the likelihood of all four observations (i.e., simply the product of all four observations’ likelihoods) is much higher for µ = 0 than for the other two values. The likelihood ratio for µ = 0 compared to µ = -1 is 4.07, and 13.43 compared to µ = 1. To conclude, we have clear evidence in favor of µ = 0 relative to these two other values of µ.
This result is not surprising. We know from standard statistical theory that the sampling error of the mean equals , meaning that the other values of µ are two units of standard error away from the true value of µ=0. Hence it would be rather unlikely to obtain strong evidence in favor of a wrong model in this case.
Let us now consider the likelihood of the same data under a selection model based on two intervals, one for negative and one for positive values of x. In this approach the likelihood is considered for each interval independently. In p-uniform* this means that an observation’s likelihood is conditional on the probability of being in that interval, given the parameters. This means that the likelihoods of the two positive observations are divided by P(X > 0), which is .841, .5, .159 for µ equal to 1, 0, -1, respectively, and that the likelihoods for the two negative observations are divided by P(X < 1), or .159, .5, .841. As the sum of the two densities equals 2, and we want to compare the likelihoods to those under the regular approach, without loss of generality we divided the resulting likelihoods by 2 to obtain:
| x | f(mu = 0) | f(mu = 1) | f(mu = 1) |
|---|---|---|---|
| -1.0556027 | 0.2285302 | 0.2367199 | 0.1520090 |
| -0.2535911 | 0.3863186 | 0.1794435 | 0.5730345 |
| 0.0251569 | 0.3988161 | 0.7433878 | 0.1474168 |
| 0.6864966 | 0.3151907 | 0.3032495 | 0.2257168 |
These densities or likelihoods are also shown in Figure 2.
Figure 2: Likelihoods of four x-values (vertical lines) for models N(-1,1) in red, N(0,1) in green, N(1,1) in blue, under selection model p-uniform* based on two intervals (until and from 0).
Note that the shape of the density for µ = 0 is unaffected in Figure 2 and equal to that in Figure 1, whereas the density for below (above) 0 is “inflated” for the normal model with µ = 1 (µ = -1). Note that “inflation” is misleading; µ is estimated merely based on observations in these two independent intervals.
Computing the likelihood ratio for µ = 0 compared to µ = -1 yields 0.072, and 0.239 compared to µ = 1. That is, the best fitting value of µ is -1! Paradoxical, as the smallest of the four observations is just below -1 (i.e., -1.056), and the other three values are well above -1…
The example suits well to provide an intuition of why the effect size estimator of the selection approaches is less precise than under the regular approach. Foremost, recall that p-uniform*’s estimate of µ is unbiased, although in this example p-uniform*’s estimate of µ will be very far off the mark. The estimate is (very) imprecise for two related reasons. First, information on the likelihood of an observation in an interval is lost, or not considered anymore. For instance, that the probability of having an observation below 0 only equals .159 if µ = 1, does no longer enter the likelihood calculations. Note that not considering this probability is good if it is incorrect, as it is incorrect to consider the regular density in case of publication bias; in our example it is suboptimal, as there is no selection bias in our example.
Second, as the two intervals are smaller than the complete interval, the likelihood function of these intervals is more sensitive to changes in the values of the observations, which also leads to less precision. For instance, consider the two positive observations in our example. As seen from Figure 2, x = 0.025 is most likely under µ = -1, whereas x = 0.686 is about equally likely under all three models. As the two positive observations are, by chance, close to 0, the estimate of µ will be (very) negative. That is, conditional on x > 0, the x-values are more likely to be just above 0 for strongly negative values of µ than for positive values of µ. For instance, for µ = -2, the likelihood for both positive observations equals 1.128 × 0.238 = 0.268, which is higher than the likelihood for µ=-1 (0.743 × 0.303 = 0.225), which means an increase in likelihood, although the probability of an observation in this interval decreases from .159 (for µ=-1) to .023 (µ=-2). But note that the probability of an observation in this interval is ignored.
4. How much does precision of estimators decrease in selection models?
We conducted a small simulation study to examine the precision of estimators for μ and σ2 of selection models, relative to the precision of a regular model. We again used the N(0,1) distribution as in our example, and estimated both the mean and variance of the distribution based on N (10, 100, 1,000, 100,000) observations and the following selection models that vary both the number intervals and the positioning of the intervals:
2_eq: (<-,0) and [0,->), each with 0.5 probability
3_eq: (<-,-0.43), [-0.43, 0.43), [0.43, ->) each with 1/3 probability
4_eq: (<-,-0.67), [-0.67, 0), [0, 0.67), [0.67, ->) each having 1/4 probability
2_un: (<-,1.96), [1.96, ->), with .025 in the last interval
3_un: (<-,-1.96), [-1.96,1.96), [1.96, ->), with .025 in first and last interval
4_un: (<-,-1.96), [-1.96,0), [0,1.96), [1.96, ->), splitting the middle interval
The “_eq” scenarios create equally large intervals with respect to the expected number of observations, whereas the “_un” scenarios correspond to selection models with unequal intervals with regions for statistical significance.
See here for the code that my colleague Robbie van Aert from the meta-research center wrote for this small simulation study, and for all the resulting tables with results as well. Here I only briefly discuss the most important results.
First, the parameters could not be estimated well for three and four intervals, in case of N=10. Hence selection models with more than two intervals are not recommended in case of a small number of observations. Clear guidelines on data requirements for selection models still need to be developed, based on research as presented here.
Second, precision of estimators decreases in the number of intervals, and precision is lower in the scenarios with equal intervals. The table below shows the ratio of the sampling variance of the selection model and of a regular model (1/N) for estimating µ.
| 2_eq | 2_un | 3_eq | 3_un | 4_eq | 4_un | |
|---|---|---|---|---|---|---|
| n = 100 | 2.906 | 1.281 | 4.711 | 1.462 | 7.527 | 4.701 |
| n = 1,000 | 2.887 | 1.132 | 5.099 | 1.256 | 7.589 | 4.439 |
| n = 100,000 | 2.767 | 1.193 | 5.153 | 1.302 | 7.324 | 3.911 |
For instance, the variance of the estimate of µ is a bit less than 3 times (if N = 100,000, 2.767) as large as this variance under a regular model with one interval. Note that precision is not much worse for two or three unequal intervals. However, data were simulated under the null-hypothesis resulting in almost all observations (95% or 97.5%) ending up in the largest interval. This may not occur in an application where the null is false, hence the estimator’s precision can be expected to be lower in most applications.
The next table shows that the precision of the variance parameter σ2 also suffers estimation in intervals, but compared to the estimation of µ (i) precision suffers less, and (ii) precision suffers most in the case of unequal intervals.
| 2_eq | 2_un | 3_eq | 3_un | 4_eq | 4_un | |
|---|---|---|---|---|---|---|
| n = 100 | 1.048 | 1.437 | 1.358 | 2.567 | 1.743 | 2.581 |
| n = 1,000 | 1.052 | 1.547 | 1.391 | 2.292 | 1.722 | 2.292 |
| n = 100,000 | 1.063 | 1.507 | 1.316 | 2.162 | 1.602 | 2.163 |
5. Conclusions
Selection models including p-uniform* provide unbiased estimates of µ and τ2 in the context of publication bias, as opposed to random-effects meta-analysis. However, selection models need sufficient data, but currently there are no clear guidelines concerning data requirements.
Accurate estimation comes at a price of lower precision, particularly for estimating µ. As precision also suffers from adding intervals to the model, intervals should only be added in case of a strong suggestion of differential publication for these intervals.
More research on how much precision of estimators of selection models suffer from adding one or more intervals to the model. This is important as we want to select the appropriate estimators for meta-analysis, estimators that balance accuracy and precision. When examining this balance, a better performance measure should be developed that than the MSE, for instance from the MSEMA family in (2).
References
Carter, E. C., Schönbrodt, F. D., Gervais, W. M., & Hilgard, J. (2019). Correcting for bias in psychology: A comparison of meta-analytic methods. Advances in Methods and Practices in Psychological Science, 2(2), 115–144. https://doi.org/10.1177/2515245919847196
Hedges, L. V., & Vevea, J. L. (2005). Selection method approaches. In H. R. Rothstein, A. J. Sutton, & M. Borenstein (Eds.), Publication bias in meta-analysis: Prevention, assessment, and adjustments. Chichester: UK: Wiley.
van Aert, R. C. M., & van Assen, M. A. L. M. (2025). Correcting for publication bias in a meta-analysis with the p-uniform* method. Manuscript submitted for publication. https://doi.org/10.31222/osf.io/zqjr9